• Teacher observation during class discussion and activities
• Work samples on whiteboards
• Exit Ticket activity

T:  This lesson is designed to meet various learning styles, mainly visual and auditory. Use the following suggestions to tailor the lesson to the needs of your students.

Routine: Group and partner work is used throughout so that students can help each other. Emphasis should be placed on communicating mathematical ideas with the specific vocabulary words appropriate to the concepts. Encourage students to create and explain real-world contexts for different graphs and equations used in the problems. The lesson requires accurate notes but also active participation. Assist students with organizational and note-taking skills to enhance the learning experience while creating a useful resource (notes).

Small Group: Struggling students can be placed in one or more small groups to get further assistance from the instructor. Use the example below. Model the thinking used to begin and work through the problem. Ask students questions designed to help you complete the steps in the problem, and allow them to ask any questions they have. Either instruct students to finish the problem where you left off or create a similar problem for them to do completely on their own.

Example Problem: Century Middle School physical education classes are planning to go on a bowling field trip. Two bowling alleys are being considered. The first bowling alley charges $6.00 per student and $9.25 per adult chaperone. The second bowling alley charges $7.25 per student and $5.50 per adult chaperone. Assign variables, write equations, find the solution set, and explain what the solution set means.

Extension: Have pairs of students write a real-world problem involving a system of equations. Students should solve the problem using each method (graphing, elimination, and substitution), and prepare a presentation including a visual display such as a poster, PowerPoint, transparency, etc. If time permits, allow students to:

• trade problems with another group and assess that group’s response.
• teach a lesson to the class or a small group using their problem.
• present their solutions including (visuals) and explain which is the most efficient method.

O:  The lesson is organized so that students learn two more ways of solving systems, in addition to the graphic method they learned in Lesson 1. They take notes on the different methods to organize their thoughts and to use as a resource while solving systems. Students practice solving systems of linear equations algebraically, both on their own and in pairs. The class works together to discuss the methods and solutions. Students are also introduced to the concepts of no solution and infinitely many solutions. The activity with mini-whiteboards or sheets of paper allows students to receive immediate feedback on their work so they can get back on track quickly.

W: This lesson introduces two new methods for solving systems of equations. Students learn how to use the substitution and elimination methods. In addition, students examine which method (graphing, substitution, or elimination) is most efficient in a variety of situations. Students learn how to recognize when a system has one solution, no solutions, or infinitely many solutions, and how this relates to efficiency.

H: “In the previous lesson we learned how systems of equations are often used in real-world situations that involve different rates of change. We also learned how to find the solution by graphing and how to check the solution. There are many different ways of getting to the same solution.”

“How many of you would rather find the sum of 478 + 478 + 478 + 478 + 478 + 478 by hand than with a calculator?” (Most will likely say the calculator would be easier or more convenient.)

“When we do a task and try to do it quickly and more easily, that is called being efficient.”

“Who has ever used a dustbuster (small handheld vacuum)? Have you ever used a full-size vacuum? When would it be more efficient to use the dustbuster rather than the vacuum? When would it be more efficient to use the vacuum rather than the dustbuster?”

“Graphs are a very useful way of visualizing a system of equations and are often used when the system is a real-world situation. Graphing worked out very efficiently for some of our examples. Can you tell me which ones?” (those with whole number or integer values for solutions)

“Did you find any of them to be frustrating or inaccurate when you graphed them?” (when the solution was nonintegral)

“Today you will learn some new, more efficient methods for finding the solution to a system of equations.”

E:  Review the walking competition problem from the previous lesson. To determine if students are thinking algebraically, ask students how they could have found the intersection point without graphing the two equations.

The following notes should be displayed on the board for students to copy 

      Three Ways to Solve a System of Equations

      1.     Graphing: used to visualize the solution to the system.

  2.    Substitution Method: used when one or both equations are written in slope-intercept form (y = mx + b)

    Example 1: The walking competition (both equations are in slope-intercept form).

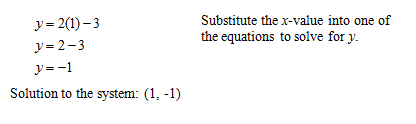
3.   Elimination Method or Linear Combination Method: used when both equations are written in standard form (Ax + By=C).

• The goal is to eliminate one of the variables in order to solve for the other.
• Elimination is done by adding the two equations together.
  • The variable being eliminated must have the same coefficient but with opposite signs.

(End of student notes.)

Solutions:  1. (4, 5); 2. (2, 4); 3. (-2, -8); 4. (-5, -2); 5. (-8, 0); 6. (0, 3)

When most have finished, have students write their work on the board. Go over the problems as a class.

Following the discussion, have students solve the following two systems as a think-pair-share activity.

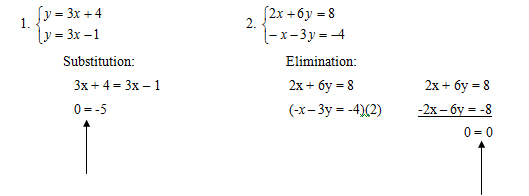
Since 0 does not equal -5, there are no solutions.                             

            Since 0 does equal 0, there are infinitely many solutions.

Ask students why the first problem has no solutions. Tell students to take a close look at the equations. Display the Systems of Linear Equations and Solutions Chart to help students answer this question and the others that follow (A1-5-2_Systems of Linear Equations and Solutions Chart.doc).  Question students using questions such as:

• “Do the equations have anything in common?”
• “Why do you think the first problem has no solutions?”
• “What would you expect the graph to look like? Graph the system of equations.”
• “Why does the second problem have infinitely many solutions?”
• “What would you expect the graph to look like? Graph the system of equations.”
• “How is the first equation related to the second equation in each problem?”

R: Provide students mini-whiteboards or paper and markers. Display the following six problems on the board or overhead. Instruct students to show their work to solve the systems of equations on their whiteboard or paper. Once they have completed a problem, ask them to hold their whiteboard/paper up in the air facing you. Tell them you will either say yes or no. If you say yes, they erase the board and go to the next problem, or they use another sheet of paper to move on to the next problem. If you say no, then they need to try the problem again. Students cannot go on to the next problem until you have said yes to their work and solution.

Emphasize to students that this is not a race. It may be helpful to tally the number of times you say yes and no to each problem, and also to make note of students who may be struggling. When everyone is done or after a predetermined amount of time, go over the problems with students and clarify misconceptions or areas of confusion.

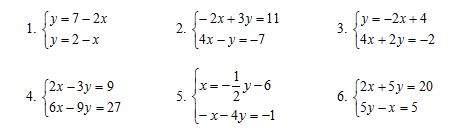
Solutions:  1. (5, -3); 2. (-1, 3); 3. no solution; 4. infinitely many solutions;
5. (-7, 2); 6. (5, 2)

E:  Pass out the exit tickets (A1-5-2_Exit Ticket.doc) to evaluate students’ understanding. “The local movie theater was celebrating its 25^th anniversary and was giving a discount on tickets. You didn’t know what the ticket prices were, but you heard two of your classmates discuss how much it cost their families to go to a movie last weekend. One student said the cost for two adults and two children was $12. Another student said the cost for three adults and four children was $20.”

     It would be useful to display the scenario on an overhead or the board.

      “What are the variables/unknowns in this situation?”

“What information do we know?”

“Make sure that you define your variables whenever you are using them for a real-world situation.”

“On your own, work on writing the system of equations for this situation, choose the most efficient method for solving it, and then explain what the solution represents in terms of the situation.”

Have students work on their own to complete the problem. They will hand their work in at the end of class. If there is time, go over the problem in class.

Answers:

1.  Write the system of equations that represents the movie ticket scenario.

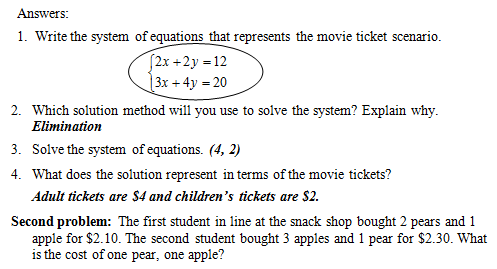
It would be useful to display the scenario on an overhead or the board.

      “What are the variables/unknowns in this situation?”

“What information do we know?”

“Make sure that you define your variables whenever you are using them for a real-world situation.”

“On your own, work on writing the system of equations for this situation, choose the most efficient method for solving it, and then explain what the solution represents in terms of the situation.”

Have students work on their own to complete the problem. They will hand their work in at the end of class. If there is time, go over the problem in class.

Answers:

1.  Write the system of equations that represents the apple and pear cost scenario.